Neural Networks

Activation Functions

Activation Functions

Limits output values
Squashing function

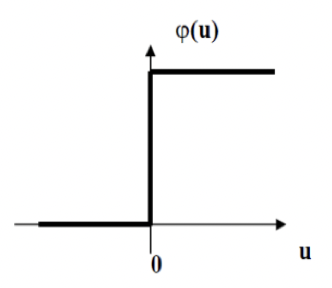
Threshold

For binary functions
Not differentiable
- Sharp rise
Heaviside function
Unipolar
- 0 <-> +1
Bipolar
- -1 <-> +1

threshold-activation

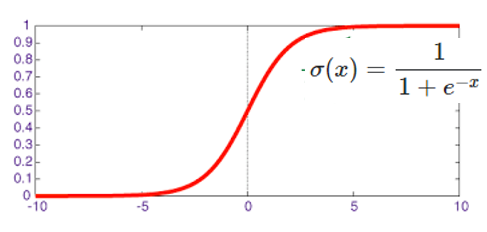
Sigmoid

Logistic function
Normalises
Introduces non-linearity
Alternative is $tanh$ $t anh$
- -1 <-> +1
Easy to take derivative $\frac d {dx} \sigma(x)= \frac d {dx} \left[ \frac 1 {1+e^{-x}} \right] =\sigma(x)\cdot(1-\sigma(x))$

sigmoid

Derivative

y_j(n)=\varphi_j(v_j(n))= \frac 1 {1+e^{-v_j(n)}}

\frac{\partial y_j(n)}{\partial v_j(n)}= \varphi_j'(v_j(n))= \frac{e^{-v_j(n)}}{(1+e^{-v_j(n)})^2}= y_j(n)(1-y_j(n))

Nice derivative
Max value of $\varphi_j'(v_j(n))$ occurs when $y_j(n)=0.5$
Min value of 0 when $y_j=0$ or $1$
Initial weights chosen so not saturated at 0 or 1

If $y=\frac u v$ Where $u$ and $v$ are differential functions

\frac{dy}{dx}=\frac d {dx}\left(\frac u v\right)

\frac{dy}{dx}= \frac {v \frac d {dx}(u) - u\frac d {dx}(v)} {v^2}

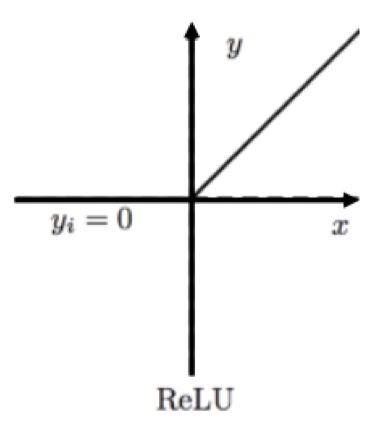
ReLu

Rectilinear

For deep networks
$y=max(0,x)$
CNNs
- Breaks associativity of successive convolutions
  - Critical for learning complex functions
- Sometimes small scalar for negative
  - Leaky ReLu

relu

SoftMax

Output is per-class vector of likelihoods #classification
- Should be normalised into probability vector

AlexNet

f(x_i)=\frac{\text{exp}(x_i)}{\sum_{j=1}^{1000}\text{exp}(x_j)}

Properties Capabilities Architectures