Interpretation

Activation Maximisation

• Synthesise an ideal image for a class
  • Maximise 1-hot output
  • Maximise SoftMax

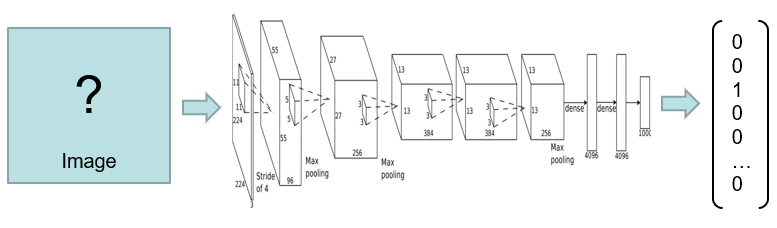
• Use trained network
  • Don’t update weights
• Feedforward noise
  • Back-propagate loss
    • Don’t update weights
    • Update image

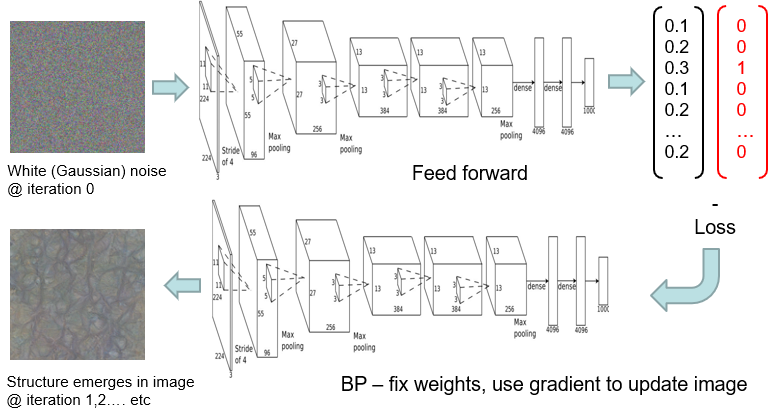
Regulariser

• Fit to natural image statistics
• Prone to high frequency noise
  • Minimise
• Total variation
  • $x^*$ is the best solution to minimise loss

• Won’t work $x^*=\text{argmin}_{x\in \mathbb R^{H\times W\times C}}\mathcal l(\phi(x),\phi_0)+\lambda\mathcal R(x)$
• Need a regulariser like above

• Beta
  • Degree of smoothing