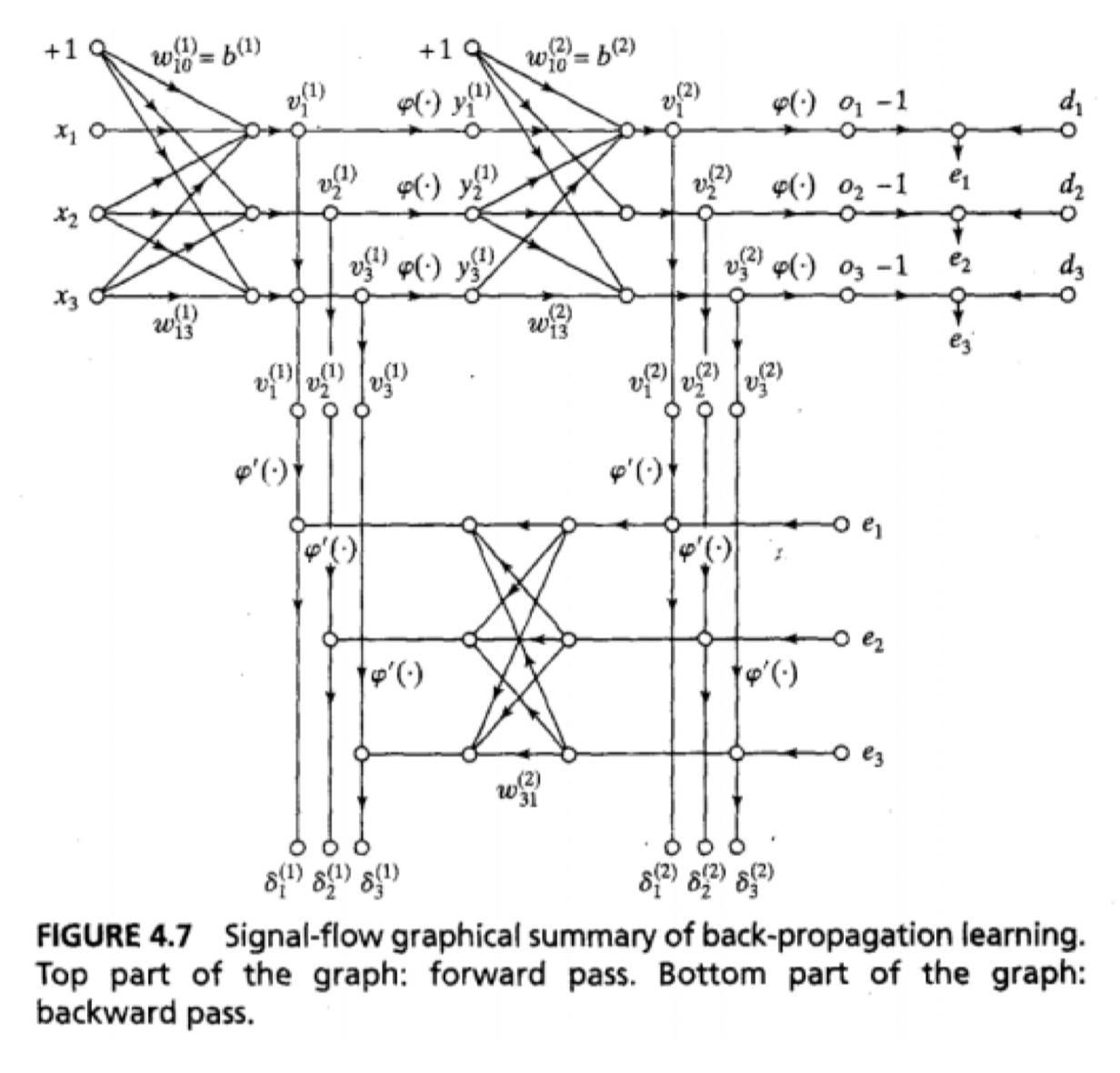
Error signal graph

1. Error Signal
   • $e_j(n)=d_j(n)-y_j(n)$
2. Net Internal Sum
   • $v_j(n)=\sum_{i=0}^mw_{ji}(n)y_i(n)$
3. Output
   • $y_j(n)=\varphi_j(v_j(n))$
4. Instantaneous Sum of Squared Errors
   • $\mathfrak{E}(n)=\frac 1 2 \sum_{j\in C}e_j^2(n)$
   • $C$ = o/p layer nodes
5. Average Squared Error
   • $\mathfrak E_{av}=\frac 1 N\sum_{n=1}^N\mathfrak E (n)$

From 4

From 1

From 3 (note prime)

From 2

Composite

Gradients

Output Local

Hidden Local

Weight Correction

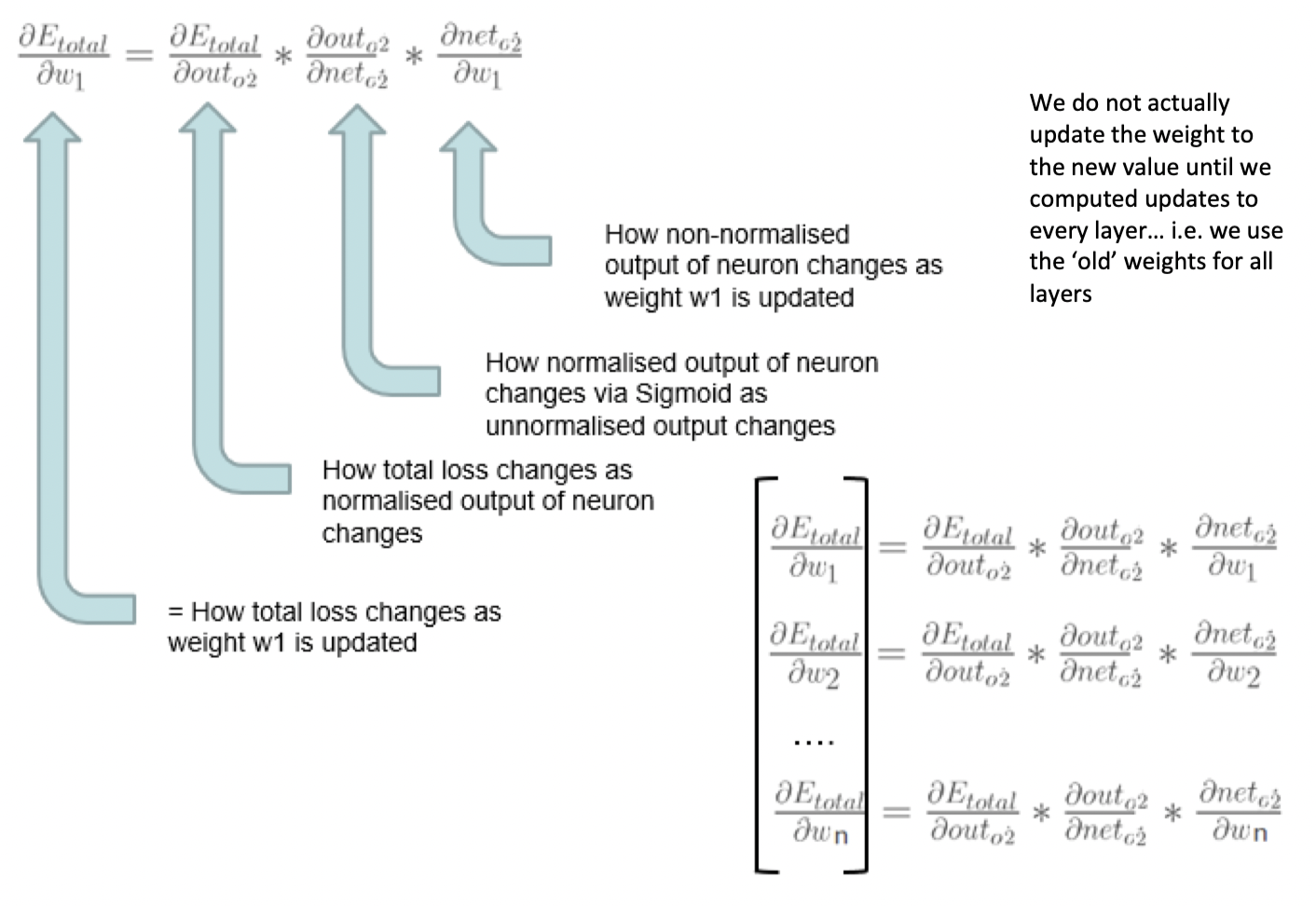
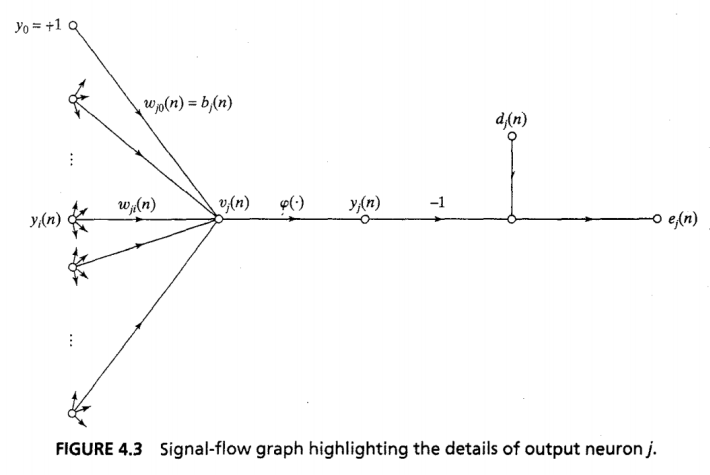
• Looking for partial derivative of error with respect to each weight
• 4 partial derivatives
  1. Sum of squared errors WRT error in one output node
  2. Error WRT output $y$
  3. Output $y$ WRT Pre-activation function sum
  4. Pre-activation function sum WRT weight
     • Other weights constant, goes to zero
     • Leaves just $y_i$
  • Collect 3 boxed terms as delta $j$
    • Local gradient
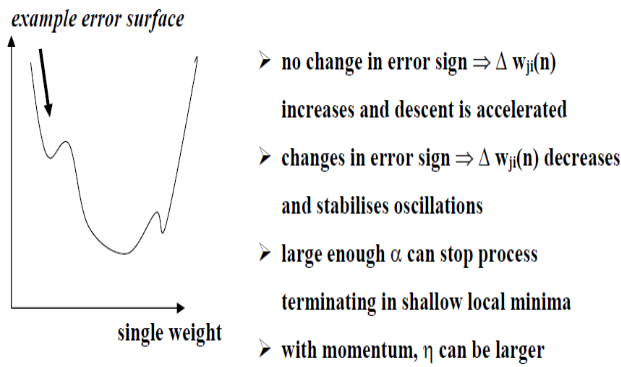
• Weight correction can be too slow raw
  • Gets stuck
  • Add momentum

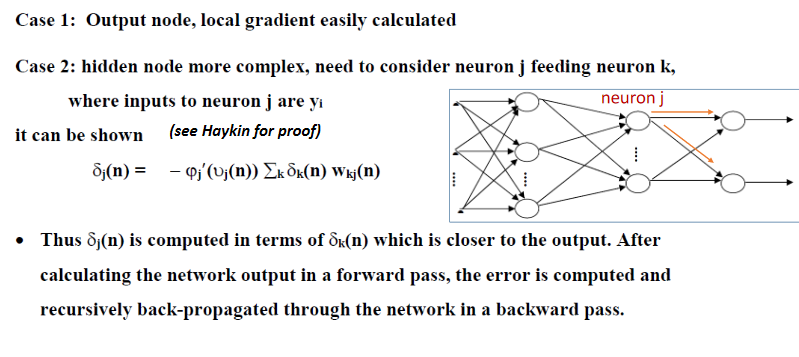
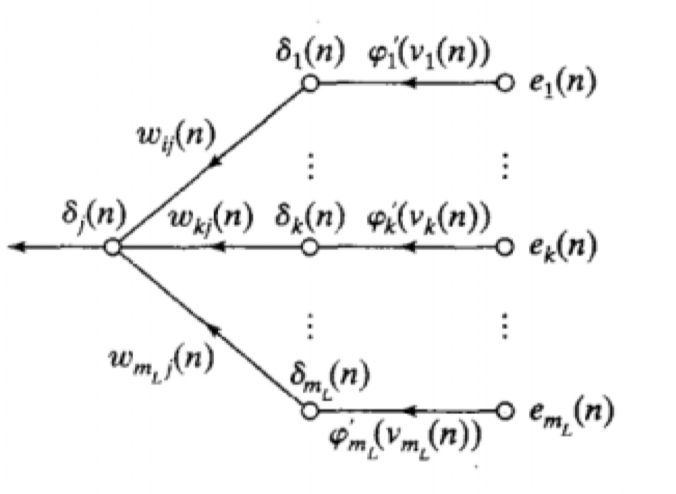
• Nodes further back
  • More complicated
  • Sum of later local gradients multiplied by backward weight (orange)
  • Multiplied by differential of activation function at node

Global Minimum

• Much more complex error surface than least-means-squared
• No guarantees of convergence
  • Non-linear optimisation
• Momentum
  • $+\alpha\Delta w_{ji}(n-1), 0\leq|\alpha|<1$
  • Proportional to the change in weights last iteration
    • Can shoot past local minima if descending quickly

$w^+_5=w_5-\eta\cdot\frac{\partial E_{total}}{\partial w_5}$