Error-Correcting Perceptron Learning

• Uses a McCulloch-Pitt neuron
  • One with a hard limiter
• Unity increment
  • Learning rate of 1

If the $n$-th member of the training set, $x(n)$, is correctly classified by the weight vector $w(n)$ computed at the $n$-th iteration of the algorithm, no correction is made to the weight vector of the perceptron in accordance with the rule:

Otherwise, the weight vector of the perceptron is updated in accordance with the rule

1. Initialisation. Set $w(0)=0$. perform the following computations for
   time step $n = 1, 2,...$
2. Activation. At time step $n$, activate the perceptron by applying continuous-valued input vector $x(n)$ and desired response $d(n)$.
3. Computation of Actual Response. Compute the actual response of the perceptron:
   $y(n) = sgn[w^T(n)x(n)]$
   where $sgn(\cdot)$ is the signum function.
4. Adaptation of Weight Vector. Update the weight vector of the perceptron:
   $w(n+1)=w(n)+\eta[d(n)-y(n)]x(n)$ where $d(n) = \begin{cases} +1 &\text{if $x(n)$ belongs to class $\mathfrak{c_1}$}\\ -1 &\text{if $x(n)$ belongs to class $\mathfrak{c_2}$} \end{cases}$
5. Continuation. Increment time step $n$ by one and go back to step 2.

• Guarantees convergence provided
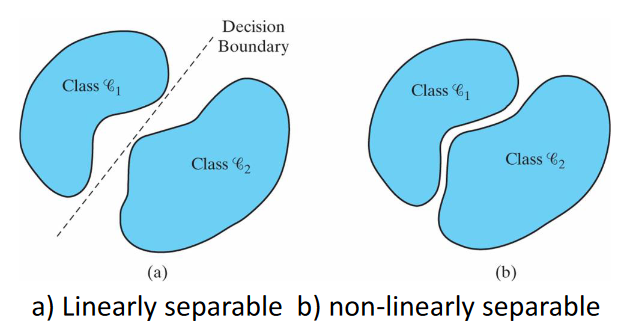
  • Patterns are linearly separable
    • Non-overlapping classes
    • Linear separation boundary
  • Learning rate not too high
• Two conflicting requirements
  1. Averaging of past inputs to provide stable weight estimates
     • Small eta
  2. Fast adaptation with respect to real changes in the underlying distribution of process responsible for $x$
     • Large eta