Wiki
AI
Pattern Matching
Dynamic Time Warping

Deterministic Pattern Recogniser Allows timescale variations in sequences for same class

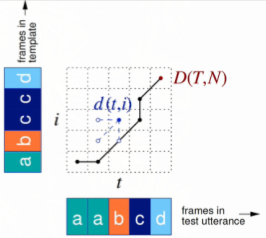
D(T,N)=min⁡t,i∑t∈1..Ti∈1..Nd(t,i)D(T,N)=\min_{t,i}\sum_{\substack{t\in1..T \\ i\in1..N}}d(t,i)
  • d(t,i)d(t,i) is distance between features from tt-th frame of test to ii-th frame of template
D(t,i)=min⁡[D(t,i−1),D(t−1,i−1),D(t−1,i)]+d(t,i)D(t,i)=\min[D(t,i-1),D(t-1, i-1),D(t-1,i)]+d(t,i)
  • Allowing transition from current and previous frame only
  • Recursive

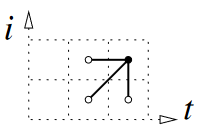
Problems

  • How much flexibility to allow?
  • How to penalise warping?
  • How to determine a fair distance metric?
  • How many templates to register?
    • How to select best ones?

Basic Algorithm

  1. Initialise the cumulative distances for t=1t=1 D(1,i)={d(1,i)for i=1,D(1,i−1)+d(1,i)for i=2,...,ND(1,i)=\begin{cases}d(1,i) & \text{for }i=1, \\ D(1, i-1)+d(1,i) & \text{for }i=2,...,N\end{cases}
  2. Recur for t=2,...,Tt=2,...,T D(t,i)={D(t−1,i)+d(t,i)for i=1,min⁡[D(t,i−1),D(t−1,i−1),D(t−1,i)]+d(t,i)for i=2,...,ND(t,i)=\begin{cases}D(t-1,i) + d(t,i) & \text{for }i=1, \\ \min[D(t, i-1), D(t-1, i-1),D(t-1,i)] + d(t,i) & \text{for }i=2,...,N\end{cases}
  3. Finalise, the cumulative distance up to the final point gives the total cost of the match: D(T,N)D(T,N)

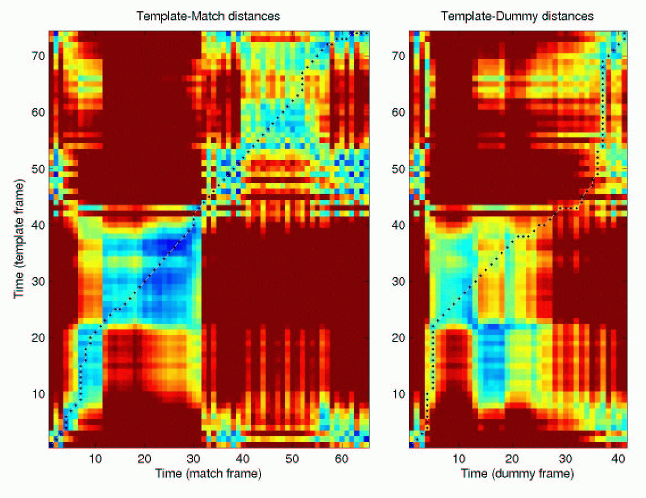
  • Euclidean distances

Distortion Penalty

  1. Initialise the cumulative distances for t=1t=1 D(1,i)={d(1,i)for i=1,d(1,i)+D(1,i−1)+dVfor i=2,...,ND(1,i)=\begin{cases}d(1,i) & \text{for }i=1, \\ d(1,i)+D(1, i-1)+d_V & \text{for }i=2,...,N\end{cases}
  2. Recur for t=2,...,Tt=2,...,T D(t,i)={d(t,i)+D(t−1,i1)+dHfor i=1,min⁡[d(t,i)+D(t,i−1)+dV,2d(t,i)+D(t−1,i−1),d(t,i)+D(t−1,i)+dH]for i=2,...,ND(t,i)=\begin{cases}d(t,i)+D(t-1,i1)+d_H & \text{for }i=1, \\ \min[d(t,i)+D(t,i-1)+d_V,2d(t,i)+D(t-1,i-1),d(t,i)+D(t-1,i)+d_H] & \text{for }i=2,...,N\end{cases}
  • Where dVd_V and dHd_H are costs associated with vertical and horizontal transitions respectively
  1. Finalise, the cumulative distance up to the final point gives the total cost of the match: D(T,N)D(T,N)
  • Allows weighting for dynamic penalties when moving horizontally or vertically
    • As opposed to diagonally

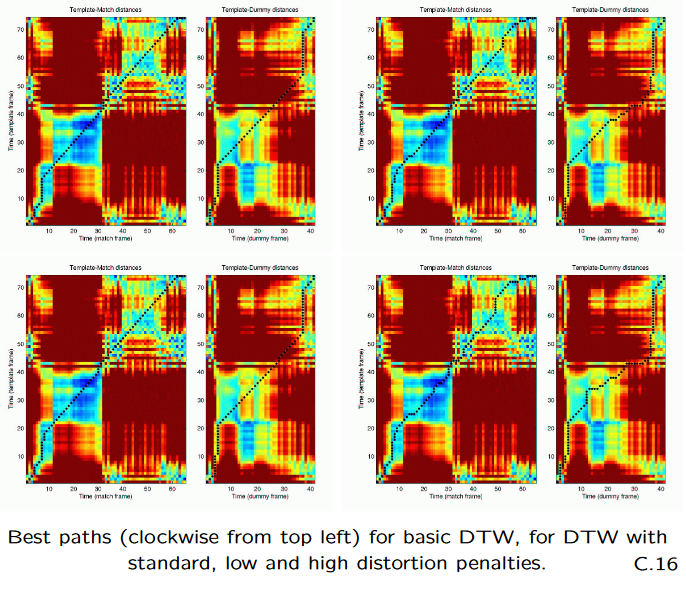
Store Best Path

  1. Initialise distances and traceback indicator for t=1t=1 D(1,i)={d(1,i)for i=1,d(1,i)+D(1,i−1)for i=2,...,ND(1,i)=\begin{cases}d(1,i) & \text{for } i=1,\\ d(1,i)+D(1,i-1) & \text{for }i = 2,...,N\end{cases} ϕ(1,i)={[0,0]for i=1,[1,i−1]for i=2,...,N\phi(1,i)=\begin{cases}[0,0] & \text{for } i=1,\\ [1,i-1] & \text{for }i = 2,...,N\end{cases}
  2. Recur for cumulative distances at t=2,...,Tt=2,...,T D(1,i)={d(t,i)+D(t−1,i)for i=1,d(t,i)+min⁡[D(t,i−1),D(t−1,i−1),D(t−1,i)]for i=2,...,ND(1,i)=\begin{cases}d(t,i)+D(t-1,i) & \text{for } i=1,\\ d(t,i)+\min[D(t,i-1),D(t-1,i-1),D(t-1,i)] & \text{for }i = 2,...,N\end{cases} ϕ(1,i)={[t−1,i]for i=1,arg⁡min⁡[D(t,i−1),D(t−1,i−1),D(t−1,i)]for i=2,...,N\phi(1,i)=\begin{cases}[t-1,i] & \text{for } i=1,\\ \arg\min[D(t,i-1),D(t-1,i-1),D(t-1,i)] & \text{for }i = 2,...,N\end{cases}
  3. Final point gives the total alignment cost D(T,N) and the end coordinates of the best path zK=[T,N]z_K=[T,N], where KK is the number of nodes on the optimal path
  4. Trace the path back for k=K−1,...,1,zk=ϕ(zk+1), and Z={z1,...,zK}k=K-1,...,1,z_k=\phi(z_{k+1}), \text{ and }Z=\{z_1,...,z_K\}
  • Stores best path

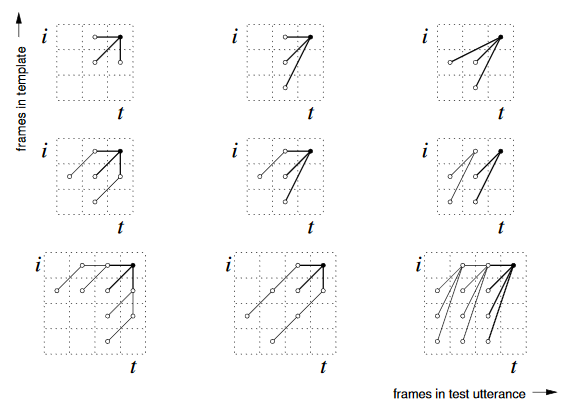
  • Vary allowable movements through grid
  • Second row for blocking multiple of the same movements in succession

Search Pruning

  • Speed up algorithm for real-time
  • Kill bad options

Gross Partitioning

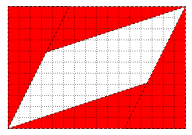
  • Too far from diagonal
  • Probably wrong or bad

Score Pruning

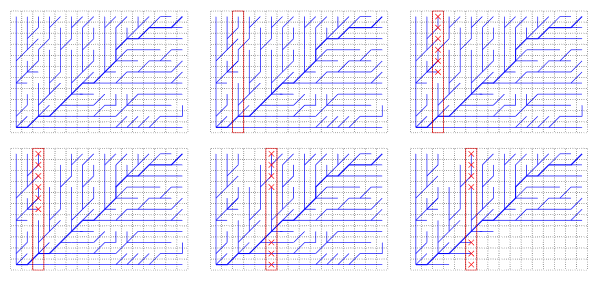
  • Examine existing branches
  • See which scores are really bad
Pattern Matching