Wiki
AI
Pattern Matching
Markov Chains

Markov Chains

Hidden Markov Models - JWMI Github Rabiner - A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition

  • Stochastic sequences of discrete states
    • Transitions have probabilities
  • Desired output not always produced the same
    • Same pronunciation

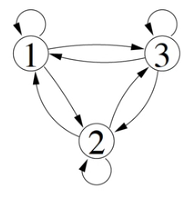
P(X∣M)=(∏t=1Taxt−1xt)ηxTP(X|M)=\left(\prod_{t=1}^Ta_{x_{t-1}x_t}\right)\eta_{x_T}

ax0x1=πx1a_{x_0x_1}=\pi_{x_1}

1st Order

  • Depends only on previous state
    • Markov assumption
P(xt=j∣xt−1=i,xt−2=h,...)≈P(xt=j∣xt−1=i)P(x_t=j|x_{t-1}=i,x_{t-2}=h,...)\approx P(x_t=j|x_{t-1}=i)
  • Described by state-transition probabilities
aij=P(xt=j∣xt−1=i),1≤i,j≤Na_{ij}=P(x_t=j|x_{t-1}=i), 1\leq i,j\leq N
  • α\alpha
    • State transition
  • For NN states
    • NN  by NN matrix of state transition probabilities

Weather

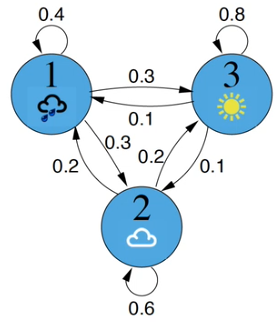
A={aij}=[0.40.30.30.20.60.20.10.10.8]A=\left\{a_{ij}\right\}=\begin{bmatrix} 0.4 & 0.3 & 0.3\\ 0.2 & 0.6 & 0.2 \\ 0.1 & 0.1 & 0.8 \end{bmatrix}

rain, cloud, sun across columns and down rows

A={πj,aij,ηi}={P(xt=j∣xt−1=i)}A=\{\pi_j,a_{ij},\eta_i\}=\{P(x_t=j|x_{t-1}=i)\}

Start/End

  • Null states
    • Entry/exit states
    • Don’t generate observations

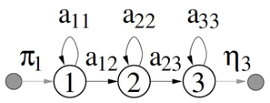
πj=P(x1=j) 1≤j≤N\pi_j=P(x_1=j) \space 1 \leq j \leq N
  • Sub jj because probability of kicking off into that state ηi=P(xT=i) 1≤i≤N\eta_i=P(x_T=i) \space 1 \leq i \leq N
  • Sub ii because probability of finishing from that state

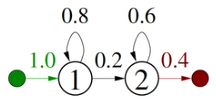
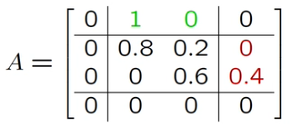
State Duration

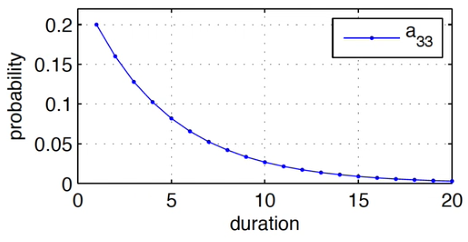
  • Probability of staying in state decays exponentially p(X∣x1=i,M)=(aii)τ−1(1−aii)p(X|x_1=i,M)=(a_{ii})^{\tau-1}(1-a_{ii})
  • Given, a33=0.8a_{33}=0.8
  • ×0.8\times0.8 repeatedly
    • Stay in state