Rank

• Number of indices
• Basis vectors per dimension/component
• 0
  • Scalar
• 1
  • Column Vector
• 2
  • Square Matrix
• 3
  • Cube matrix

Matrices are not inherently rank-2 tensors. Matrices are just the formatting structure. The tensor described by the matrix must follow the transformation rules to be a tensor

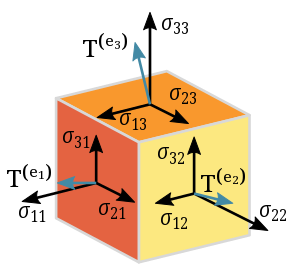
Transformation Rules

1. Transforms like a tensor
2. Invariant to a change in coordinate system
   • Components change according to mathematical formulae

Dimension

• Dimensionality to the rank = number of components

An $n$-rank tensor in $m$-dimensional space is a mathematical object that has $n$ indices and $m^n$ components and obeys certain transformation rules

From <wolfram>