• Poles
  • X
  • Let $X(z) = inf$
    • Let $1/X(z) = 0$
  • Roots of denominator
• Zeros
  • O
  • Let $X(z) = 0$
  • Roots of numerator
• In complex (Z for speech) domain

Magnitude Response From Pole/Zeros MIT Pole Zero

Representation of rational transfer function, identifies

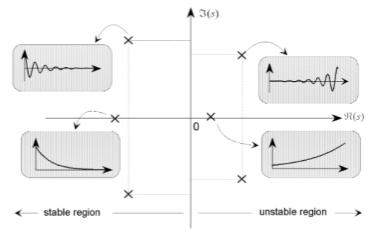
• Stability
• Causal/Anti-causal system
• ROC
• Minimum phase/Non minimum phase

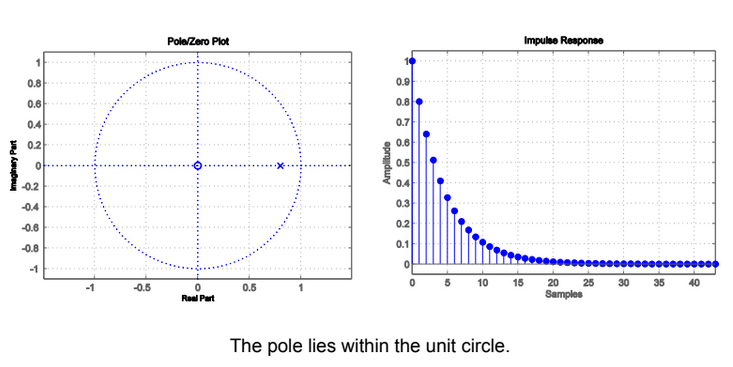
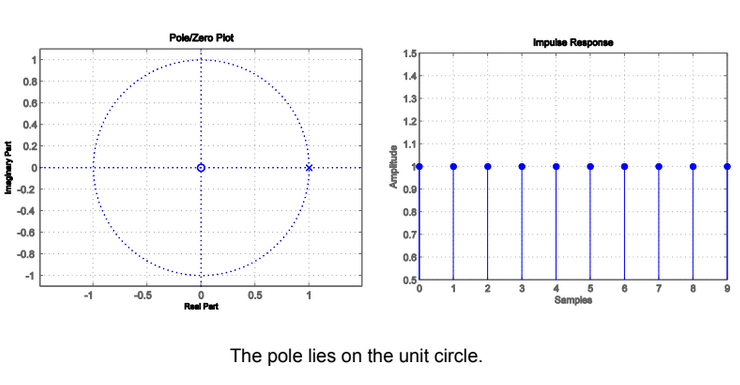
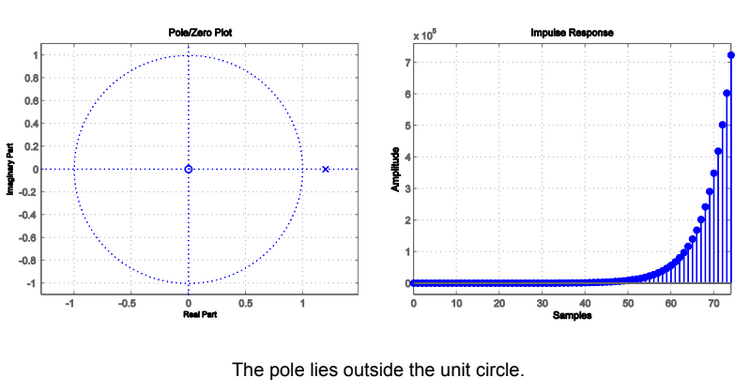
BIBO Stable

• All poles of H must lie within the unit circle of the plot
• If we give an input less than a constant
• Will get an output less than some constant

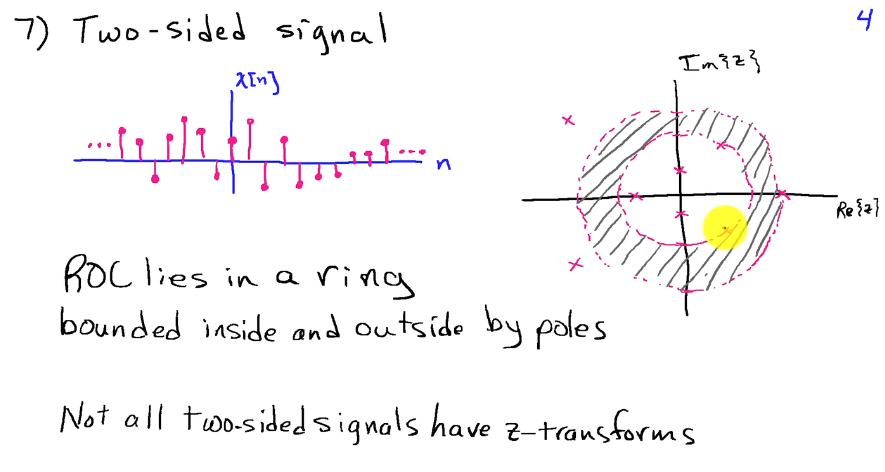
Region of Convergence

• Depends on whether causal or anti-causal
• Cannot contain poles
  • Goes to infinity

Continuous

1. If includes imaginary axis
   • BIBO stable
   • All poles must be left of i axis
2. Rightwards from pole with largest real-part (not infinity)
   • Causal
3. Leftward from pole with smallest real-part (not -infinity)
   • Anti-causal

Discrete

1. If includes unit circle
   • BIBO stable
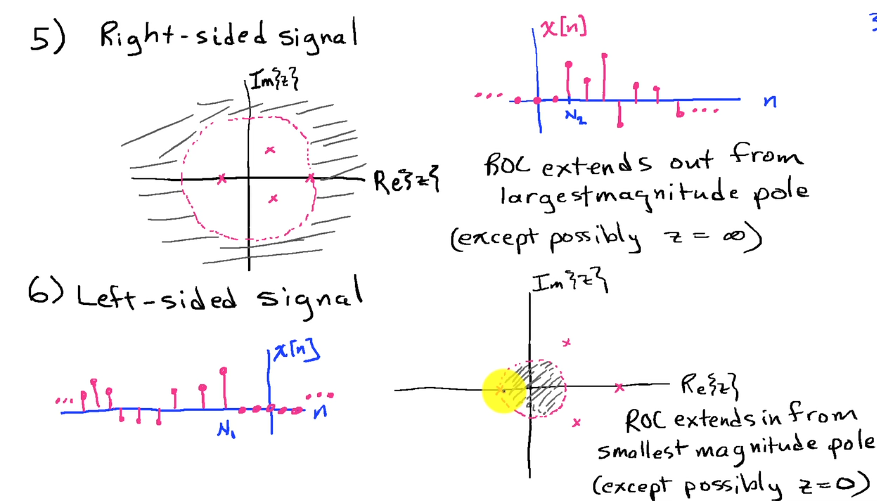
2. Outward from pole with largest (not infinite) magnitude
   • Right-sided impulse response
   • Causal (if no pole at infinity)
3. Inward from pole with smallest (nonzero) magnitude
   • Anti-causal

Sinusoidal when complex pair

• $e^{-j\omega}$
• Euler’s for oscillating Exponential when on the axis
• Decays, no $i$ in the exponent